Topic Modeling – Latent Semantic Analysis (LSA) and Singular Value Decomposition (SVD):

• Singular Value Decomposition is a Linear Algebraic concept used in may areas such as machine learning (principal component analysis, Latent Semantic Analysis, Recommender Systems and word embedding), data mining and bioinformatics
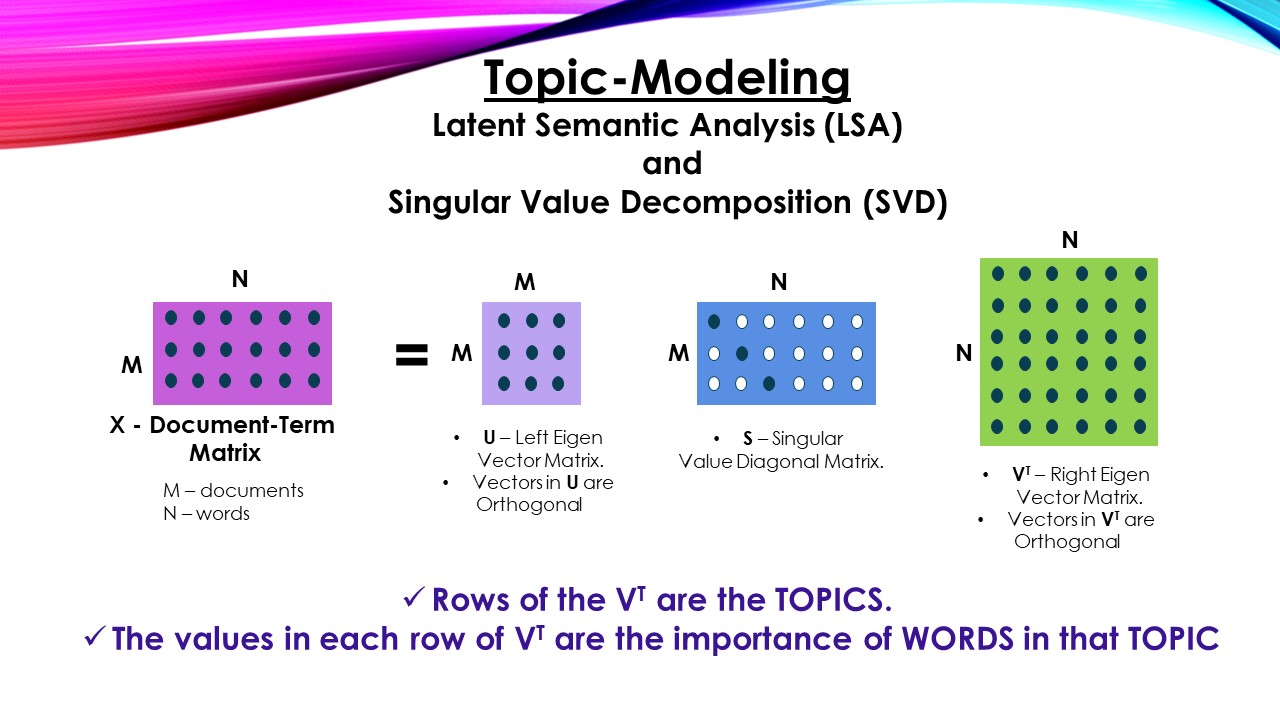
• The technique decomposes given matrix into there matrices, let’s look at programmer’s perspective of the technique.

[codesyntax lang=”python”]

import numpy as np
import pandas as pd

[/codesyntax]

Let’s take a small dataset and create Document-Term matrix.

• Note: Need to build Term-Document matrix For Query Retrieval in IR task.

[codesyntax lang=”python”]

documents = ["I enjoy Machine Learning", "I like NLP", "I like deep learning"]

from sklearn.feature_extraction.text import CountVectorizer

cv = CountVectorizer(ngram_range=(1, 1))
X = cv.fit_transform(documents).toarray()

[/codesyntax]

X is the Document-Term Matrix, “DOCUMENTS” – are the “rows” and “TOKENS” – are the “columns” of the matrix

Output: array([[0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 0, 1],
       [1, 0, 1, 1, 0, 0]], dtype=int64)

[codesyntax lang=”python”]

cv.get_feature_names()

[/codesyntax]

Output: ['deep', 'enjoy', 'learning', 'like', 'machine', 'nlp']

[codesyntax lang=”python”]

cv.vocabulary_

[/codesyntax]

Output: {'enjoy': 1, 'machine': 4, 'learning': 2, 'like': 3, 'nlp': 5, 'deep': 0}

Notation

• “*” – for Matrix multiplication
• V.T – to denote Transpose of matrix V

Now SVD will decompose rectangular matrix X into there matrices. Namely U, S and V.T (V transpose)

• U – the left Eigen vector (orthogonal) matrix, the vectors extract “Document-to-Document similarity”.
• V – the right Eigen vector (orthogonal) matrix, the vectors extract “Strength of Two Different Words Occurring in one Document” (may or may-not be co-occurrence)
• S – the Eigen Values (diagonal) matrix, explains variance ratio.
  

  Before we understand how U, V, S extract relation strengh or explain variance ratio. Let’s understand on how to decompose X.

• To decomposing any matrix, we should use Eigen Vectors, Eigen Values decomposition.
• A matrix is eligible to apply Eigen decomposition only when it is a *square and symmetric matrix.
• We can get a SQUARE, SYMMETRIC matrix by multiplying “X.T with X” or “X with X.T”, we can decompose these (np.dot(X.T,X) and np.dot(X,X.T) and get U, S, V matrixes.
  

  Why to multiply “X.T with X” or “X with X.T”?, Why to decompose “X.T with X” or “X with X.T”?

• Suppose that X is decomposed as U S V.T
  • i.e., X = U * S * V.T
• Now let’s see what is X.T multiplied by X
  • X.T * X = (U * S * V.T).T * (U * S * V.T)
  •           = (V * S.T * U.T) * (U * S * V)
  •           = V * S.T * (U.T * U) * S * V)
  •           = V * S.T * (I) * S * V # as U is an orthogonal matrix U.T * U = I
  •           = V * (S.T * S) * V
  •           = V * S^2 * V # as S is diagnoal matrix S.T * S is S-square
• We got V * S^2 * V, when we multiply X.T with X, where X is in decomposed form (U * S * V.T), Hence, when we decompose X.T * X, we get values of matrix V and S^2
• Now let’s see what is X multiplied by X.T
  • X * X.T = (U * S * V.T) * (U * S * V.T).T
  •           = (U * S * V) * (V.T * S.T * U)
  •           = (U * S * (V * V.T) * S.T * U)
  •           = U * S * (I) * S.T * V # as U is an orthogonal matrix U.T * U = I
  •           = U * (S.T * S) * U
  •           = U * S^2 * U # as S is diagnoal matrix S * S.T is S-square
• We got U * S^2 * U, when we multiply X.T with X, where X is in decomposed form (U * S * V.T), Hence, when we decompose X * X.T, we get values of matrix U and S^2
• Bottom line: To find U, S and V, we need to find Eigen Decoposition of X.T * X and X * X.T

X.T * X is word similarity matrix, the (i, j) position in X.T * X will quantify the overlap of Word-i and Word-j. Number of Documents in which both words i and j occur. (This inference is based out of Document-Term matrix, if it is Tf-IDF, then the inference would be different)

[codesyntax lang=”python”]

np.dot(X.T, X)

[/codesyntax]

Output: array([[1, 0, 1, 1, 0, 0],
       [0, 1, 1, 0, 1, 0],
       [1, 1, 2, 1, 1, 0],
       [1, 0, 1, 2, 0, 1],
       [0, 1, 1, 0, 1, 0],
       [0, 0, 0, 1, 0, 1]], dtype=int64)

X * X.T is document similarity matrix, the (i, j) position in X * X.T will quantify the similarity of Document-i and Document-j. This analogy suits best with Tf-IDF scores.

[codesyntax lang=”python”]

np.dot(X, X.T)

[/codesyntax]

Output: array([[3, 0, 1],
       [0, 2, 1],
       [1, 1, 3]], dtype=int64)

The rows in sigular vector matrix V.T are the topics and values in the row denote strenght of words in the topic.

[codesyntax lang=”python”]

U, s, Vh = np.linalg.svd(X)

terms = cv.vocabulary_
for i, component in enumerate(Vh):
    terms_components = zip(terms, component)
    sorted_terms = sorted(terms_components, key=lambda x:x[1], reverse=True)[:3] # take features for topic
    print("topic : ", i)
    for term_socres in sorted_terms:
        print(10*" ", term_socres[0])
    print(50*'*')

[/codesyntax]

Output:
topic :  0
           deep
           nlp
           machine
**************************************************
topic :  1
           nlp
           machine
           learning
**************************************************
topic :  2
           enjoy
           learning
           like
**************************************************
topic :  3
           nlp
           enjoy
           like
**************************************************
topic :  4
           nlp
           learning
           like
**************************************************
topic :  5
           deep
           enjoy
           nlp
**************************************************

–By

L Venkata Rama Raju